National mortality tables are crucial inputs to the quantification of mortality and longevity risks. In the absence of data specific to insured or pension populations, national mortality tables are based on general population data. Recent work by Milliman demonstrates problems with the reliability of these reference tables, including false cohort effects, and offers methodological improvements for their construction. This White Paper presents both historical perspectives and new solutions to this problem.
Since the publication of the first mortality table in 1662, attributed to John Graunt, the scientific community has developed an increasing interest in the measurement of the distribution of lifetimes in a given population. Two major innovations occurred in the 19th century: (1) the practical one was the campaigns of large-scale national censuses, and (2) the theoretical one was the development of a precise graphical formalization of life trajectories within a population by Lexis (1875) and his contemporaries. See Figure 1 for examples of these original representations.
Figure 1: Two examples of the Lexis diagram by Lexis (1875)

These innovative graphics helped understanding of two major characteristics of the construction of mortality tables at the scale of a given country:
- The structure of mortality around two dimensions, age, and time
- The dynamic nature of the evolution of the population beyond simple aging, especially removals by deaths and renewal by births
These two characteristics lead to theoretical and practical difficulties still unresolved today; thus, there is no methodological consensus regarding the construction of mortality tables based on the observation of a population at periodic but isolated points in time. In this context, observations from censuses lead to major problems of reliability in estimates of national general population mortality rates as implemented in practice. Faced with these difficulties, it is necessary to put population dynamics at the core of the analysis of mortality and longevity risks.
Recent awareness about reliability issues
The analysis of cohort effects has long fascinated the actuarial community; these effects correspond to the observation that specific generations can have longevity characteristics different from those of the previous and the following ones. It is through the study of such cohort effects that Richards (2008) has suggested the idea of possible anomalies in the calculation of national mortality rates. Specifically, based on observations of tables for England and Wales, and in particular neighboring generations of 1919, he conjectured that sudden changes in fertility patterns may cause errors in the calculation of mortality rates; thus, the cohorts born in years with erratic numbers of births could produce incorrect mortality levels in the table.
To understand the impact of fluctuations in births, we must consider and compare the bases for the numerator and the denominator in the computation of annual mortality rates: for a given year and age, the mortality rate is the ratio between the number of deaths and the exposure-to-risk. The number of deaths at a given age is captured using death certificates, but the exposure-to-risk requires a detailed assessment of the total exposure period during which individuals would have been assigned that age if they had died in the year being studied. In the absence of continuous observation of the population, the exposure-to-risk is approximated from annual records extracted from the census. The standard approximation of the exposure-to-risk by age is the average between the populations by age at the beginning and at the end of the year. However, the presence of birth fluctuations in the pair of calendar years when this age group was born makes this linear approximation inexact. (Another common approximation would consider the population by age only at the beginning of the year, which is also inexact.) This inexactness has been noted since 2007 in the technical documentation associated with the Human Mortality Database, see Wilmoth et al. (2007). The Human Mortality Database is now the standard reference provider of mortality tables for 38 countries and regions worldwide. Because the direction of the inexactness repeats every year for a given birth cohort, the calculated mortality rates over time will be consistently distorted, either overstated or understated. However, the inexactness tends to be reflected in adjoining birth cohorts in the opposite direction, and the calculated improvement from one birth cohort to the next cohort is doubly affected for each age through which both birth cohorts pass, so a false cohort effect with high magnitude can appear.
Correcting mortality tables based on fertility data
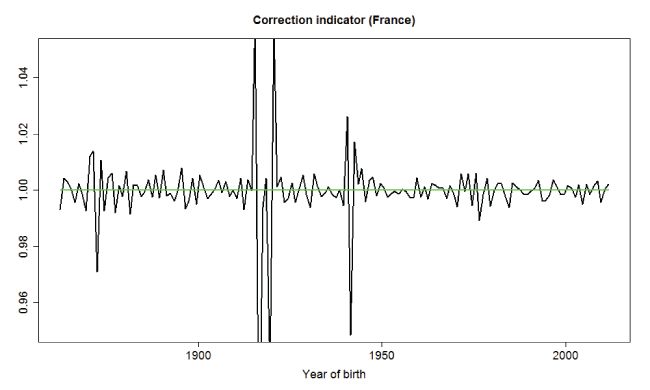
The conjecture of Richards (2008) about the 1919 cohort effect has since been confirmed by Cairns, Blake, Dowd and Kessler (2016) who worked with the example of England, using monthly and quarterly birth numbers to quantify the approximation errors in the mortality rate calculations of the ONS (Office for National Statistics). New developments, carried out at Milliman, see Boumezoued (2016), highlighted the universal nature of these apparently isolated (and actually false) cohort effects, which are unfortunately present in most period tables of the Human Mortality Database (HMD). Faced with the wide presence of these anomalies, our first work used the monthly fertility data provided by the Human Fertility Database (HFD), which is the project on fertility inspired by the success of the HMD. When the history of these fertility data is deep enough (which is the case for approximately 10 countries in the HMD, see countries in blue in Figure 4 in next section), our first approach allowed us to build a quality indicator measuring the relative error associated with the estimated exposure-to-risk. Figure 2 shows such a quality indicator for the example of the French mortality table. When the quality indicator for a given generation (year of birth in x-axis) is close to 1, it indicates a satisfactory quality (that is, satisfactory exactness or validity) for the mortality rates for this generation. However, a deviation from this level quantifies an overestimation or underestimation of the associated death rates. In this graph, it appears that the generations with major data anomalies in France are those born on the edge of war periods (in the neighborhoods of 1915, 1920, 1940 and 1945). We are directly measuring mortality rate shocks due to birth patterns.
Figure 2: Quality indicator of the French mortality table for each generation
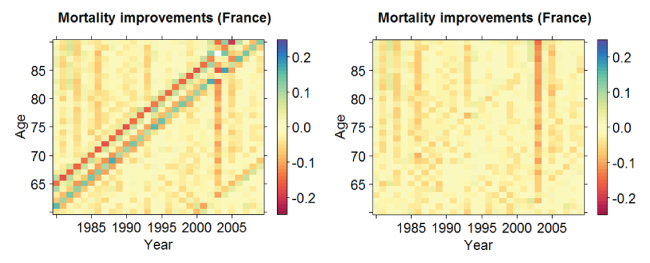
In the approach proposed by Boumezoued (2016), this indicator is then used to produce the corrected tables for several countries of the HMD; an example of the impact of this correction is shown in Figure 3 on mortality improvement rates for France. The first major consequence of the correction of the mortality rates to recognize monthly birth patterns is the removal of apparently isolated (and actually false) cohort effects that have previously been included in the risk analysis and calibration of stochastic mortality models.
Figure 3: Improvement rate for France before and after correction
Although this method provides corrected mortality tables for those countries in the HMD with suitable HFD data, we wanted to deal with countries for which fertility histories were not deep enough. Indeed, even in the absence of relevant monthly fertility data, we extended the statistical method to provide a total review of the HMD period tables.
New developments to tackle the lack of monthly fertility data
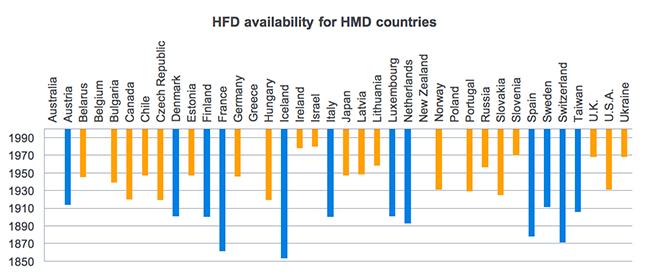
To get a clear view of the availability of fertility histories, Figure 4 presents the availability of HFD monthly fertility records for each country of the HMD. Countries without a bar show that fertility data are unavailable, whereas for other countries the bar indicates the deepness of the monthly fertility records available, through their starting year. In particular, the bar for countries for which the fertility history starts before 1918 is highlighted in blue. The year 1918 was chosen as a criterion because this allowed us to correct the abnormal cohort effects around 1920. The bar is highlighted in orange for countries in which fertility records are not deep enough.
Figure 4: Availability of HFD monthly fertility records for each country of the HMD
The original method from Boumezoued (2016) requires monthly fertility data and is thus applicable to the countries highlighted in blue in Figure 4. To avoid this restriction, further work has been performed at Milliman to extend the correction process to the other countries with insufficient histories and, therefore, could not use the original method to correct the generations of interest (highlighted in orange in Figure 4). We developed several alternative methods for the reconstruction of the quality indicator and then tested and compared them. More precisely, we developed three regression methods with the intention of expressing the correction indicator as a function of explanatory variables in a penalized-regression procedure based on the following:
- The fertility experience of other countries in blue,
- The smoothness of the corrected mortality table.
The key ideas underlying components i) and ii) are the following:
- What are the other countries (in blue) showing similar fertility patterns that can then be used to predict the quality indicator?
- What is the quality indicator that best reduces, after correction, the cohort irregularities of the crude mortality table?
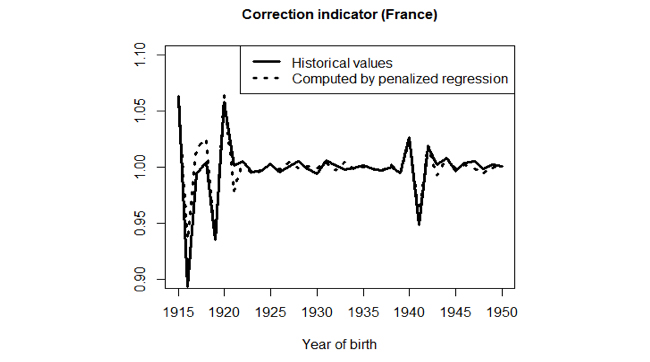
Interestingly, the statistical method that provided the best results is the one based only on criterion ii). That is, the best method incorporated the crude mortality table as the only input to produce the corrected table and did not require any fertility records. An example of the prediction based on this method applied to France is depicted in Figure 5 as the dotted line. The plain solid line in Figure 5 provides the comparison to the true observed quality indicator, either of which can be used to produce the corrected mortality table. While it is better to use the original method for countries with sufficient fertility data, the new method is not a bad approximation for these countries, and the new method is the only approximation available to improve the mortality tables for the other countries.
Figure 5: Backtesting result of the selected reconstruction method
Another interesting feature of this new method is that it provides simultaneously both the quality indicator and the output corrected table, by means of the penalized regression approach. Based on this statistical approach, it is now possible to produce corrected tables for most countries provided in the HMD, which will largely eliminate false cohort effects that had previously misled the calibration of stochastic mortality models.
Updating national mortality tables for the general population: What are the consequences for the insurance market?
The correction of national mortality rates, especially for the generations born in periods with high fertility volatility, has implications for various risk assessments. Eliminating apparently isolated cohort effects directly involves changes to the level of mortality rates, upward or downward, for the generations considered if actuaries use general population mortality rates, rather than mortality rates derived only from experience on insured lives, for their base case assumptions. For France, the magnitude of these changes is particularly high; the order of relative change can reach up to 6%, as shown in Figure 2. But France is not the only country with high order errors; we see them in the data of England and Wales, Italy, Germany, and the United States, among others. As false cohort effects are eliminated, actuaries should revisit the choice of stochastic mortality models used to produce forecasts, in particular, those that include a cohort component. Only true cohort effects should be allowed to remain.
Another major implication from these analyses of the corrected mortality tables goes beyond the consideration of specific generations. Indeed, calculating the corrected historical volatility of mortality improvement rates over the last 30 years shows a significant reduction from those based on uncorrected mortality tables, especially at ages over 60. Observed volatility is reduced when artificially high and low levels of mortality in the history are corrected. The reliability of mortality tables is crucial for quantifying the volatility of mortality and longevity risks. Even companies whose basic mortality assumptions come from observing insured lives still have to develop their assumptions regarding mortality improvement and mortality volatility from observing general population national mortality tables, at least in part.
In conclusion, our corrections to national mortality tables should be accepted as a challenge by the insurance market and related securitization markets to integrate these corrections coherently into their internal processes when assessing mortality and longevity risks.
References
- Boumezoued, A. 2016. Improving HMD mortality estimates with HFD fertility data. HAL preprint: https://hal.archives-ouvertes.fr/hal-01270565v1. Presented at the Longevity 12 conference, Chicago, September 2016; http://www.cass.city.ac.uk/longevity-12.
- Cairns, A.J.G., D. Blake, K. Dowd and A.R. Kessler. 2016. Phantoms Never Die: Living with Unreliable Population Data. Journal of the Royal Statistical Society, Series A (Statistics in Society), 179(4): 975–1005.
- Graunt, J. 1662. Natural and Political Observations Made Upon the Bills of Mortality. John Martin, London.
- Human Mortality Database. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available at www.mortality.org or www.humanmortality.de
- Human Fertility Database. Max Planck Institute for Demographic Research (Germany) and Vienna Institute of Demography (Austria). Available at www.humanfertility.org.
- Lexis, W. 1875. Einleitung in die Theorie der Bevolkerungsstatistik. Strassburg: Triibner.
- Richards, S.J. 2008. Detecting year-of-birth mortality patterns with limited data. Journal of the Royal Statistical Society: Series A (Statistics in Society), 171(1): 279-298.
- Wilmoth, J.R., K. Andreev, D. Jdanov and D.A. Glei. 2007. Methods Protocol for the Human Mortality Database. University of California, Berkeley, and Max Planck Institute for Demographic Research, Rostock. URL: http://mortality.org [version 31/05/2007.
Milliman makes no representations or warranties to the reader with respect to the information contained in this document ("Information") or to any other person or entity, as to the accuracy, completeness or merchantability of the Information. The reader of this document should not construe any of the Information as investment, legal, regulatory, financial, accounting or other advice and persons should consult qualified professionals before taking any specific actions. Milliman shall not be liable to the reader of the Information or any person or entity under any circumstances relating to or arising, in whole or in part, from any circumstance or risk (whether or not this is the result of negligence), or, for any losses, damages or other damages caused in connection with the publication of the Information or its distribution. The holder of this document agrees that it shall not use Milliman’s name, trademarks or service marks, or refer to Milliman directly or indirectly in any media release, public announcement or public disclosure, including in any promotional or marketing materials, customer lists, referral lists, websites or business presentations without Milliman’s prior written consent for each such use or release, which consent shall be given in Milliman’s sole discretion.
This Information contained therein is protected by Milliman’s and the authors’/co-authors’ copyrights and must not be modified or reproduced without express consent.
©2017 Milliman, Inc. All rights reserved.